M-ary trees
M-ary tree is a tree data structure in which each node has no more than m children. I have already mentioned M-ary trees in an earlier blog post. I’ve also written about the left child right sibling representation. In this blog post I want to write about M-ary trees in greater detail.
Introduction
M-ary tree is a generalization of a binary tree, where every node has M or less children (i.e. binary tree is an M-ary tree, with M = 2). Following image shows an example of an M-ary tree, with M = 3.

If every node of an M-ary tree has either M or 0 children, then the tree is called a full M-ary tree. If every leaf node of a full M-ary tree is at the same depth, the tree is said to be perfect. If all levels except the last one are full (i.e. every non-leaf node has M children), the tree is said to be complete.
Traversal
Similarly as with binary trees, we have:
- Pre-order traversal - visit a node and then traverse the subtrees rooted at its children (one at a time) going from left to right.
- Post-order traversal - recursively traverse all subtrees rooted at the children (starting from left to right) first and then visit the root node.
- In-order traversal - traverse the left subtree, visit the root node and then traverse the right subtree.
In order to do the in-order traversal we must first define the notion of left and right subtree. Standard way of doing this, when having M > 2 children, is to divide the list of child nodes into two non-overlapping groups which will constitute the left and the right subtree.
- left subtree:
- right subtree:
Applications
M-ary trees have many applications which include:
- Represent a file system data structure (with nodes representing files or folders).
- Parse and grammar trees for natural language processing applications
- Abstract syntax trees for representing the structure of a program code.
- Use in image processing and mesh generation
- Use in game engines for rendering and collision detection
- Color quantization
- and many more…
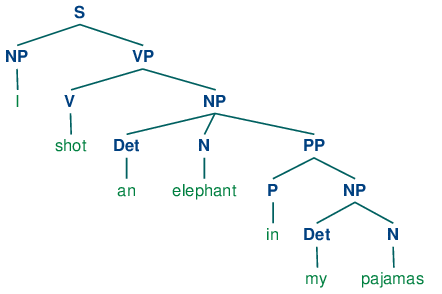
Following image shows an example of a grammar tree.
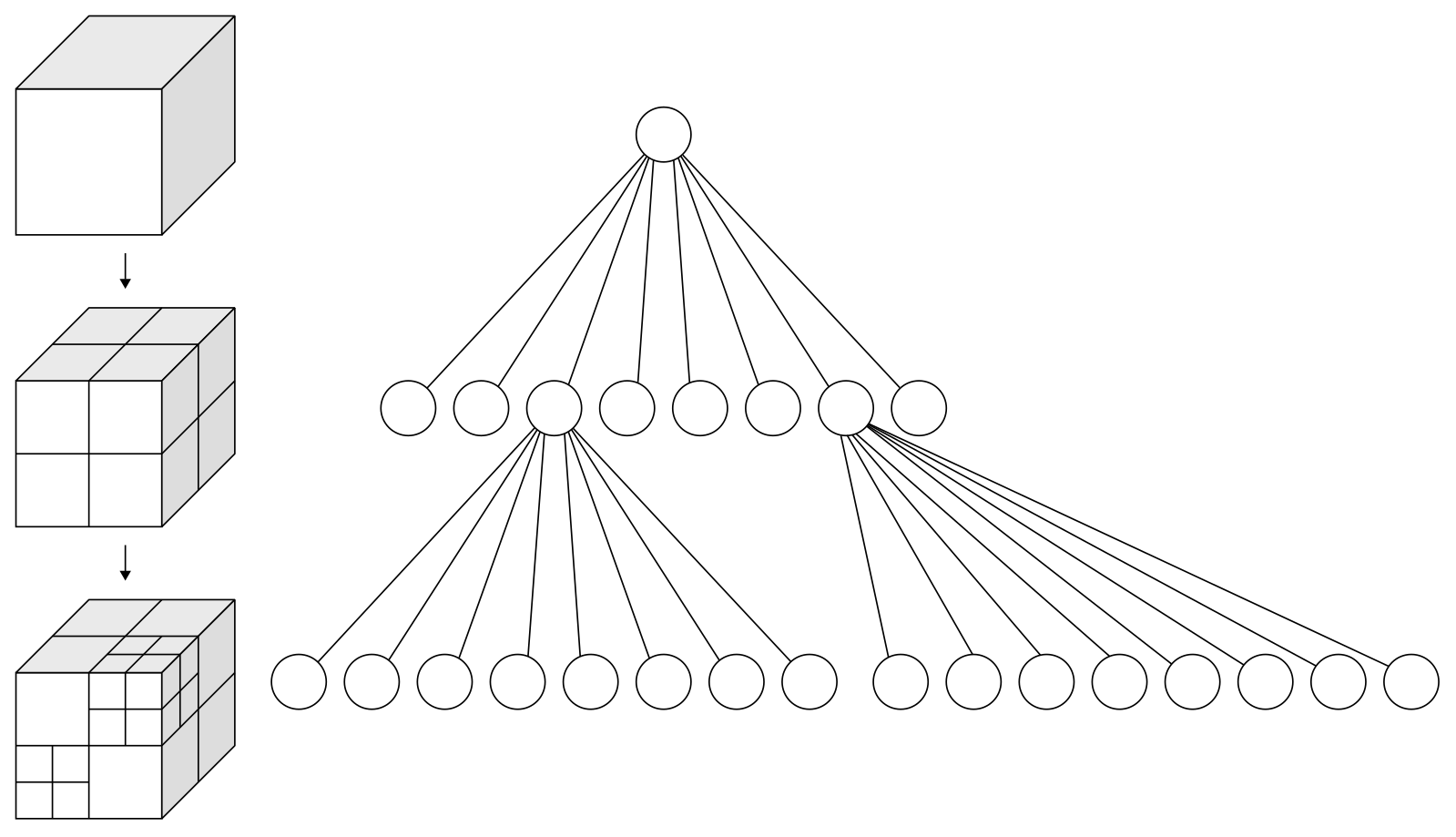
The following image shows an octree (M = 8) used for 3D rendering.
Conclusion
General M-ary trees have many applications, ranging from computer science and compiler design to 2D/3D image processing and rendering. It is very important to have a general M-ary tree data structure in Pharo to be used as a starting point for building interesting projects in different areas.