Prelude to Trees
One of the most important collections to be included in Pharo is the tree data structure and its variants. Here we give a brief introduction to rooted trees that we will build upon in the remainder of this Summer of Code. Main references for this part will be the following two books - “Introduction to Algorithms”, Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein and “Algorithms”, Robert Sedgewick and Kevin Wayne.
We start with some basic terminology for rooted trees:
-
Root
The top (first) node in a tree.
-
Child
A node directly connected to another node when moving away from the root.
-
Parent
A node directly connected to another node when moving towards the root.
-
Siblings
A set of nodes with the same parent.
-
Descendant
A node reachable by repeated proceeding from parent to child. Also known as subchild.
-
Ancestor
A node reachable by repeated proceeding from child to parent.
-
Leaf node
A node with no children.
-
Branch node
A node with at least one child.
-
Degree
For a given node, its number of children. A leaf is necessarily degree zero.
-
Edge (Branch)
The connection between two node (a parent and a child).
-
Path
A sequence of nodes and edges connecting a node with a descendant.
-
Level
The level of a node is defined as: 1 + the number of edges between the node and the root.
-
Depth
The depth of a node is defined as: the number of edges between the node and the root.
-
Height of node
The height of a node is the number of edges on the longest path between that node and a descendant leaf.
-
Height of tree
The height of a tree is the height of its root node.
-
Forest
A forest is a set of disjoint trees.
Rooted Trees
Rooted trees are usually represented as linked data structures (similar to linked lists), where every node has a key field and pointers/references to other (child) nodes. Based on the application, other representations are also possible. Common operations that can be performed on trees are:
- Insertion - new nodes can be inserted in between other two nodes, or added after a leaf node.
- Deletion - an existing node can be removed from the tree. This operation is not always unique.
- Traversal - visit each node in a tree by recursively visiting each subtree. There are different algorithms depending on the order in which the nodes are visited.
Binary Trees
The simplest example of rooted tree data structures are binary trees. In the case of binary trees, each node (x) contains the key value, and a pointer to its left (lc[x]) and right child (rc[x]) node, as well as a pointer to its parent node (p[x]). If p[x] = nil, then x is the root node. Similarly, if lc[x] = rc[x] = nil, then x is a leaf node.
Binary search trees are special data structures that allow a fast lookup, addition and removal of items. They keep their keys in sorted order, so that lookup and other operations can be done in logarithmic time (by using the principle of binary search). Following picture shows an example of a binary search tree.
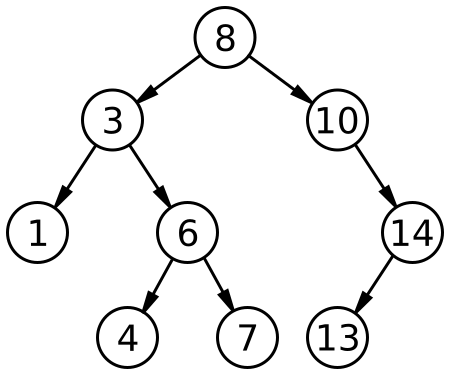
Each time we visit a node, we decide (based on the key value) to continue searching in the left or right subtree. This means that each comparison will on average eliminate half of the possible options. Binary trees can be used to implement dynamic sets or lookup tables that allow for search by key.
A binary search tree that automatically keeps its height small is called a self-balancing binary search tree. Following pictures shows an example of a height-balanced tree.

There are several different kinds of self-balancing search trees, the most important being the AVL trees and the Red-Black trees. Self-balancing trees are very useful for implementing mutable ordered lists, associative arrays, priority queues, sets …
General and Unbounded trees
Binary tree model can easily be extended to a general tree model, where every node may have more then two child nodes. If each node can have at most m children (child_1, …, child_m), we have bounded m-ary trees. Following picture shows an example of an arbitrary m-ary tree.

When the number of children is unbounded - we have unbounded trees (rooted trees with unbounded branching). In the case of unbounded trees, or in the case of m-ary trees where nodes have a small number of children (as seen in the previous picture), we may waste a lot of memory. Luckily, binary trees can be used to represent trees with arbitrary number of children by using the child-sibling representation (aka Left-child right-sibling binary tree).
Image reference:
All images presented in this post are taken from Wikipedia. All links are provided in-text.