Self-Balancing Trees
Most operations on binary search trees (BST) take time proportional to the height of the tree. Arbitrary deletions and insertions can produce an unbalanced tree (e.g. a tree can degenerate into a linked list). BSTs that automatically keep the height of the tree small are called self-balancing trees.
Self-balancing trees are flexible data structures that can be extended to perform new operations and are usually used for implementing more complex data structures such as mutable ordered lists, associative arrays, sets … “Self-balancing” is done by performing simple transformations on the tree (e.g tree rotations), when inserting and deleting nodes in order to keep the height small.
Tree Rotation
Tree rotation is an operation on a binary tree that changes the structure of the tree but maintains the order of the elements. Tree rotation is used to decrease the height of the tree by moving a smaller subtree down and a larger subtree up. When performing a rotation it is important that:
-
in-order traversal of leaves must be same before and after (the order of leaves cannot change)
-
maintain the main property of BSTs - right child is greater than the parent and the left child is less than the parent.
The following figure shows an example of a right rotation, and its inverse - the left rotation.

In order traversal:
Left tree: ((A,P,B),Q,C)
Right tree: (A,P,(B,Q,C))
The pseudo code for right and left rotation is:
Right rotation of Node Q:
Let P be Q's left child.
Set Q's left child to be P's right child.
[Set P's right-child's parent to Q]
Set P's right child to be Q.
[Set Q's parent to P]
Left rotation of Node P:
Let Q be P's right child.
Set P's right child to be Q's left child.
[Set Q's left-child's parent to P]
Set Q's left child to be P.
[Set P's parent to Q]
In the following animation, triangles represent subtrees, while circles represent nodes that are rotated.

In the previous example, one subtree (the side which is rotated) increases the height by one, while the other subtree decreases its height. This makes tree rotation useful for rebalancing a tree, by applying rotations to nodes whose left child and right child differ in height by more than 1. Self-balancing trees apply these operations automatically. In the reminder of this post we will briefly review some common self-balancing trees.
AVL Trees
AVL self-balancing tree, named after its inventors (Adelson-Velsky and Landis) is a tree where the height of any two subtrees (of any node) differ at most by 1. If at any time they differ by more than one, rebalancing is done to fix this. After each deletion or insertion (which is done as with any BST) we check the balance factor for the ancestor nodes and if they differ from 1 or -1, we apply rotation to fix this.
Following animation shows insertion of several elements into an AVL tree.

Following example shows AVL rotation strategy:

Red-Black Trees
Each node in a red-black tree has an extra bit (which is interpreted as red or black color). These bits are used to ensure the tree remains approximately balanced during insertion and deletion. Leaf nodes do not contain data (NIL) and are black. The root is usually black, and if a node is red then both its children are black. Every path from a given node to any of its descendants contains the same number of black nodes. By following these constraints, the height of the tree is approximately balanced. A red-black tree is similar to a structure of a B-tree of order 4.
Example of Red-black tree is shown in the following figure:

B-Trees
B-Tree is a generalization of the BST, where a node can have more than two children. It is used for storage systems like databases and file systems. All nodes have a variable number of child nodes within a predefined range. When inserting or deleting nodes the internal nodes may be joined or split. B-trees require less balancing then self-balancing BSTs, but require more space.
A B-tree representation of a red-black tree is given in the following figure:

An example of inserting nodes in a B-tree is shown in the following figure:
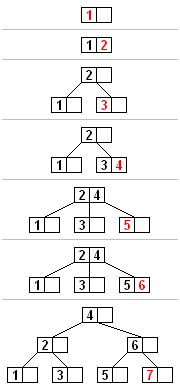
Image reference:
Image presented in this post is taken from Wikipedia and HackerRanks. Links is provided in-text.