Pharokeepers

Graphs #2

This was an exciting week. I finished the implementation of my first layout.

Let us continue with exploring graphs. By now we understand the basics, so we will go a step further. One of the reasons why, by using graphs we can accomplish so much, is that graphs have a set of algorithms for traversing them, two of which are especially well known, BFS and DFS.

First, we explain what traversing means.
The word definition is: travel across or through. In the context of graphs, traversing means moving through the graph, visiting nodes (vertices) by using the edges.

BFS - breadth first search

Single-source shortest paths: Given a graph and a source vertex s, support queries of the form Is there a path from s to a given target vertex v? If, so find a shortest such path (one with a minimal number of edges). ¹

This is what we are looking for: the shortest path from source s to given vertex v. The method for solving this is using BFS.

What does BFS do?
Let’s explain on an example.

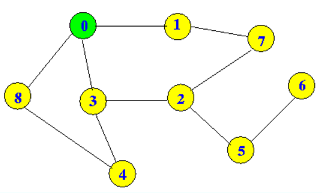
Source vertex is 0, so BFS algorithm, takes this vertex first. Now he visits all his neighbours, that have not been visited before, in our example that would be 1, 3 and 8. When a vertex has no more new neighbours to visit, it is discarded, and the first of his neighbours is taken (in our case that is 1). Now the process repeats. We are visiting all neighbours, by from vertex 1.

So the example continues like this:

0->1, 0->3, 0->8 no more neighbours;
1->7 no more neighbours;
3->2, 3->4 no more neighbours;
8, there are no neighbours, that haven’t been visited so far;
7, there are no neighbours, that haven’t been visited so far;
2->5, no more neighbours;
4, there are no neighbours, that haven’t been visited so far;
5->6, no more neighbours.

With this we have finished our algorithm and visited all vertices.

Now if we choose one vertex for a goal, like 4, we can just follow the path to it, and this will be the shortest one existing.

Path: 0->3->4

This kind of algorithm is used by navigation for finding the shortest path from one place to another.
So you can see the amount of problems that are solved easily because of them.

Jun 14, 2019, by Nina Medić